什么是计算?
在讲什么是计算之前,我们需要来了解一样更加基础的东西。你先来想一想,数学里面最基础的知识是什么呢? 答案很简单,就是数数,我们最先学会的数学不就是数一二三四五吗?
数字是怎么来的?
原始人是如何数数的?
我们先一起回到原始时代,来看看数学最早是怎么产生的。
在那个原始时代,那个时候人类还没有文字、没有数学,原始人都一起住在山洞里面,每天靠打猎、采集水果为生。
住在一起有个问题,我要是白天去打猎的话,那我存在家里的食物,就得防止它被别人偷了。
打个比方说:我好不容易弄到一堆水果🍉,还没吃完,我把它存到我的洞穴里面,白天我出去打猎了,那晚上我回到家的时候,万一我的水果少了怎么半?我怎么才能知道我的水果有没有少?
这时候数数就要出场了,如果我会数数,我早上出门前先数一数我的水果,我有9个水果,那我现在只需要记住“9”这个数字就行了。
等我打了一天的猎,晚上回到家,只要“9”这个数字没有忘记,那我就能一直精确的记得我的水果有多少,我只需要再去数一遍水果就能知道我的水果到底有没有少了。这就是数学一个很重要的点,它是精确的。
但是数数可没有那么简单,原始人要学会数数得有两个最基本的思想,这两个思想非常的高级,一般人上了大学都没学过。
离散
第一个思想叫做离散。离散的意思很简单,就说要把原来连在一起的东西给它分开,离散就是数数的基础。
你想象一下,那个原始人去数一堆水果的时候,他得做一个动作,先从那个水果里面拿出一个水果,放到一边说这是1,再拿出一个放到一边说这是2.
这个把一堆混在一起的水果一个一个拿出来的动作,就相当于在把一堆水果分开,这个动作就叫做离散。如果没有离散,原始人就不可能去数数。
抽象
数数还需要的第二个思想叫做抽象。具体的说,就是要把不同的东西看成是一样的,在数水果这件事情里面就是要把不一样的水果看成是一样的。
比如,你要是仔细观察的话,你会发现那些水果有的大、有的小、有的红、有的绿。
可是我们如果把这些水果看成是不一样的,我们觉得红色的水果和绿色的水果不是一个东西,那我们就没有办法把它们放在一起数了。
所以,把不一样的东西抽象成一样的东西,这个思想也是数数的基础
离散和抽象之所以重要,是因为使用它们可以把混成一团的事物分解成一个一个最基本的单元,这样就可以把复杂的事情变得非常简单,变得容易分析。
计算的本质
手指算数
每个人都做过计算,只是大部分人都没有理解自己在做什么。回想一下幼儿园(大概四岁)的时候,妈妈问你:“帮我算一下,4+3 等于几?” 你掰了一会手指,回答:7。当你掰手指的时候,你自己就是一台简单的计算机。
不要小看了这手指算术,它蕴含着深刻的原理。计算机科学植根于这类非常简单的过程,而不是复杂的高等数学。
现在我们来回忆一下这个过程。这里应该有一段动画,但现阶段还没有。请你对每一步发挥一下想象力,增加点“画面感”。
- 当妈妈问你“4+3 等于几”的时候,她是一个程序员,你是一台计算机。计算机得到程序员的输入:4,+,3。
- 听到妈妈的问题之后,你拿出两只手,左手伸出四个指头,右手伸出三个指头。
- 接着你开始自己的计算过程。一根根地数那些竖起来的手指,每数一根你就把它弯下去,表示它已经被数过了。你念道:“1,2,3,4,5,6,7。”
- 现在已经没有手指伸着,所以你把最后数到的那个数作为答案:7!整个计算过程就结束了。
符号和模型
这里的幼儿园手指算术包含着深刻的哲学问题,现在我们来初步体会一下这个问题。
当妈妈说“帮我算 4+3”的时候,4,+,3,三个字符传到你耳朵里,它们都是符号(symbol)。符号是“表面”的东西:光是盯着“4”和“3”这两个阿拉伯数字的曲线,一个像旗子,一个像耳朵,你是不能做什么的。你需要先用脑子把它们转换成对应的“模型”(model)。这就是为什么你伸出两只手,一只手表示 4,另一只表示 3。
这两只手的手势是“可操作”的。比如,你把左手再多弯曲一个手指,它就变成“3”。你再伸开一根手指,它就变成“5”。所以手指是一个相当好的机械模型,它是可以动,可操作的。把符号“4”和“3”转换成手指模型之后,你就可以开始计算了。
你怎么知道“4”和“3”对应什么样的手指模型呢?因为妈妈以前教过你。十根手指,对应着 1 到 10 十个数。这就是为什么人都用十进制数做算术。
我们现在没必要深究这个问题。我只是提示你,分清“符号”和“模型”是重要的。
计算图
在计算机领域,我们经常用一些抽象的图示来表达计算的过程,这样就能直观地看到信息的流动和转换。这种图示看起来是一些形状用箭头连接起来。我在这里把它叫做“计算图”。
对于以上的手指算术 4 + 3,我们可以用下图来表示它:
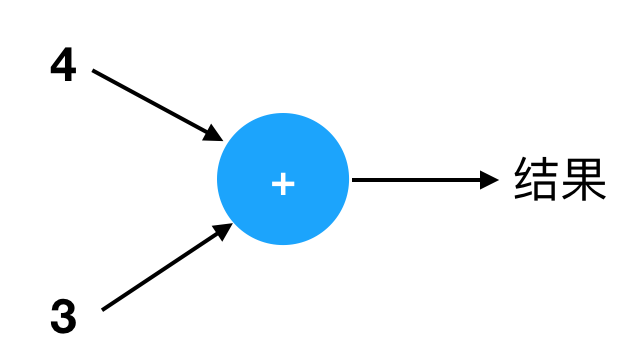
图中的箭头表示信息的流动方向。说到“流动”,你可以想象一下水的流动。首先我们看到数字 4 和 3 流进了一个圆圈,圆圈里有一个“+”号。这个圆圈就是你,一个会做手指加法的小孩。妈妈给你两个数 4 和 3,你现在把它们加起来,得到 7 作为结果。
注意圆圈的输入和输出方向是由箭头决定的,我们可以根据需要调整那些箭头的位置,只要箭头的连接关系和方向不变就行。它们不一定都是从左到右,也可能从右到左或者从上到下,但“出入关系”都一样:4 和 3 进去,结果 7 出来。比如它还可以是这样:
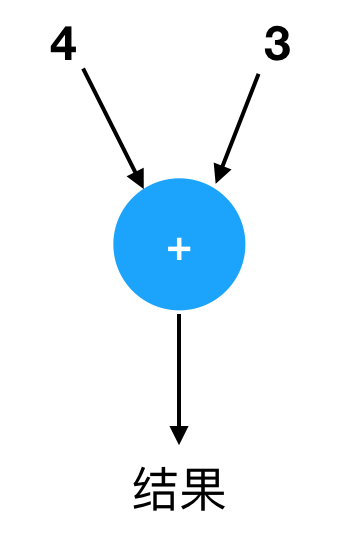
我们用带加号的圆圈表示一个“加法器”。顾名思义,加法器可以帮我们完成加法。在上个例子里,你就是一个加法器。我们也可以用其他装置作为加法器,比如一堆石头,一个算盘,某种电子线路…… 只要它能做加法就行。
具体要怎么做加法,就像你具体如何掰手指,很多时候我们是不关心的,我们只需要知道这个东西能做加法就行。圆圈把具体的加法操作给“抽象化”了,这个蓝色的圆圈可以代表很多种东西。抽象(abstraction)是计算机科学至关重要的思维方法,它帮助我们进行高层面的思考,而不为细节所累。
表达式
计算机科学当然不止 4 + 3 这么简单,但它的基本元素确实是如此简单。我们可以创造出很复杂的系统,然而归根结底,它们只是在按某种顺序计算像 4 + 3 这样的东西。
4 + 3 是一个很简单的表达式(expression)。你也许没听说过“表达式”这个词,但我们先不去定义它。我们先来看一个稍微复杂一些的表达式:
2 * (4 + 3)
这个表达式比 4 + 3 多了一个运算,我们把它叫做“复合表达式”。这个表达式也可以用计算图来表示:
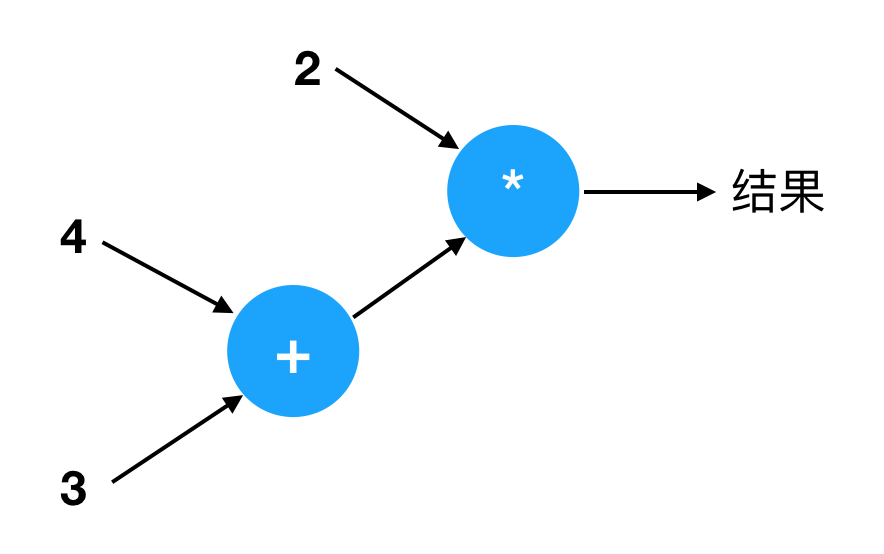
你知道它为什么是这个样子吗?它表示的意思是,先计算 4 + 3,然后把结果(7)传送到一个“乘法器”,跟 2 相乘,得到最后的结果。那正好就是 2 * (4 + 3) 这个表达式的含义,它的结果应该是 14。
为什么要先计算 4 + 3 呢?因为当我们看到乘法器 2 * ... 的时候,其中一个输入(2)是已知的,而另外一个输入必须通过加法器的输出得到。加法器的结果是由 4 和 3 相加得到的,所以我们必须先计算 4 + 3,然后才能与 2 相乘。
小学的时候,你也许学过:“括号内的内容要先计算”。其实括号只是“符号层”的东西,它并不存在于计算图里面。我这里讲的“计算图”,其实才是本质的东西。数学的括号一类的东西,都只是表象,它们是符号或者叫“语法”。从某种意义上讲,计算图才是表达式的本质或者“模型”,而“2 * (4 + 3)”这串符号,只是对计算图的一种表示或者“编码”(coding)。
这里我们再次体会到了“符号”和“模型”的差别。符号是对模型的“表示”或者“编码”。我们必须从符号得到模型,才能进行操作。这种从符号到模型的转换过程,在计算机科学里叫做“语法分析”(parsing)。我们会在后面的章节理解这个过程。
我们现在来给表达式做一个初步的定义。这并不是完整的定义,但你应该试着理解这种定义的方式。稍后我们会逐渐补充这个定义,逐渐完善。
定义(表达式):表达式可以是如下几种东西。
- 数字是一个表达式。比如 1,2,4,15,……
- 表达式 + 表达式。两个表达式相加,也是表达式。
- 表达式 - 表达式。两个表达式相减,也是表达式。
- 表达式 * 表达式。两个表达式相乘,也是表达式。
- 表达式 / 表达式。两个表达式相除,也是表达式。
注意,由于我们之前讲过的符号和模型的差别,为了完全忠于我们的本质认识,这里的“表达式 + 表达式”虽然看起来是一串符号,它必须被想象成它所对应的模型。当你看到“表达式”的时候,你的脑子里应该浮现出它对应的计算图,而不是一串符号。这个计算图的画面大概是这个样子,其中左边的大方框里可以是任意两个表达式。
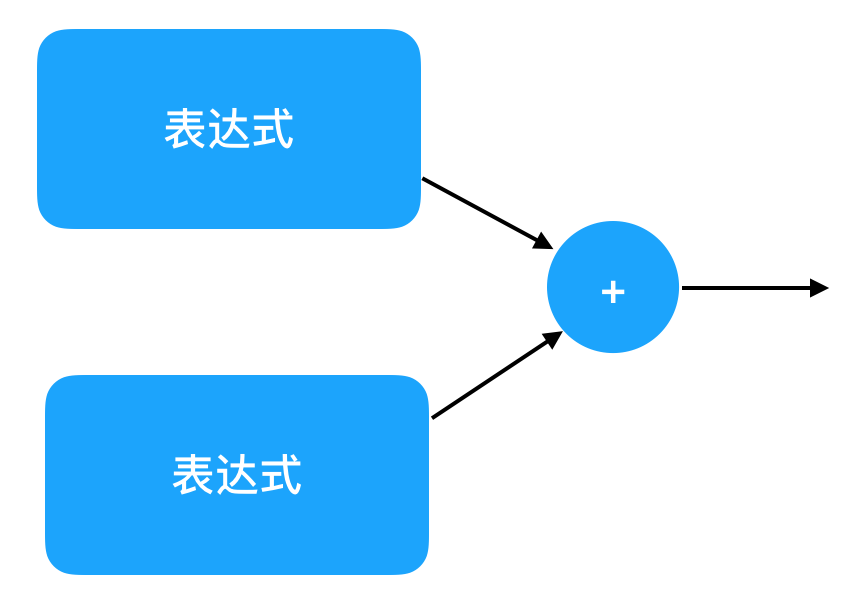
是不是感觉这个定义有点奇怪?因为在“表达式”的定义里,我们用到了“表达式”自己。这种定义叫做“递归定义”。所谓递归(recursion),就是在一个东西的定义里引用这个东西自己。看上去很奇怪,好像绕回去了一样。递归是一个重要的概念,我们会在将来深入理解它。
现在我们可以来验证一下,根据我们的定义,2 * (4 + 3) 确实是一个表达式:
- 首先根据第一种形式,我们知道 4 是表达式,因为它是一个数字。3 也是表达式,因为它是一个数字。
- 所以 4 + 3 是表达式,因为 + 的左右都是表达式,它满足表达式定义的第二种形式。
- 所以 2 * (4 + 3) 是表达式,因为 * 的左右都是表达式,它满足表达式定义的第四种形式。